頂点を用いた同側法 　 　前ページで、SS値を求める際に、対角の頂点より重心を使った方が実装上楽と書いた。 　しかし頂点を使う方法にも興味深い事情が隠れているので、まずそれを確認しておきたい。 　以降、頂点を使った同側法をExcel上で実装したものを見ながら検討する。 　ssm_2d_tri_v.xlsx　(9.93 KB) 　 　セルB2～E3に各点の座標を入力すると、H14に内外判定結果を出力する。 　B2～E3の各セルには「範囲の名前を付ける」によって、それぞれ ax、bx、…などと名前をつけてあり、以降の計算式で利用している。 　A5～D12のエリアは、各直線の標準形 ax + by + c = 0 の a、b、c の値を算出している。ただしこれらの値にゼロ以外の同一の実数をかけてもやはり同じ直線を表すから、算出する組み合わせは条件を満たすものの一例である。 　計算式は、例えば直線ABの場合、 　　　　　　a =ay-by 　　　　　　b =bx-ax 　　　　　　c =ax*by-bx*ay 　としてある。 　F5～H12のエリアは、ss値の算出を行っている。 　ここで、s( AB, C ) などと書いてあるのは、直線AB の　ax + by + c の x, y に点Cの座標を代入した値を表す。 　この場合、s( AB, C ) と s( AB, P )　は同符号であり、したがって両者を乗じた結果の ss( AB ) は正である。 　これは、直線ABについて点Cと点Pは同じ側にあることを表す。このあたりの計算式は単純なので省略する。 最後にH14のIF文で判定している。計算式は 　 =IF(OR(H6<0,H9<0,H12<0),"Outer",IF( OR(H6=0,H9=0,H12=0),"onEdge","Inner")) である。問題の点が辺上にあるか、頂点上にあるかの区別は省略している。 以上、ごく簡単な計算だけで内外判定が行えていることが確認いただけたと思う。 　さて、ここで興味深いことに、s( AB, C )、s( BC, A )、s( CA, B )　の値はいずれも19で等しい。 これは例えば直線ABの ax + by + c の a、b、c、x、y に、それぞれ 　　a =ay-by、b =bx-ax、c =ax*by-bx*ay、x = cx、y= cy を代入して整理すると 　(ax*by-bx*ay) + (bx*cy-by*cx) + (ay*cx-ax*cy) となるが、 　直線BC、直線CAのいずれでもこの式に帰着するためである。 　なお、ax*by-bx*ay、 bx*cy-by*cx、ay*cx-ax*cy 　という３つの値は、それぞれ直線AB、直線BC、直線CAの　c値になっている。 　また、これらは点A、点B、点Cの位置ベクトルを考えた時に、これらのベクトルの外積のz成分でもある。 　さらに、もともと | s( AB, C ) |　を　\( \sqrt{ a^2 + b^2} \)　で割ったものが直線ABと点Cの距離、すなわち三角形ABCの底辺を辺ABと考えた時の高さになること、さらにこの場合の　\( \sqrt{ a^2 + b^2} \)　が辺ABの長さに等しくなることを考えると、 　| s( AB, C ) | ÷ 底辺ABの長さ = 三角形ABCの高さ 　という関係が成り立つことになり、したがって 　　| s( AB, C ) |　は三角形ABCの面積の２倍の値になっている。 　| s( BC, A ) | も、| s( CA, B ) |　もやはり同一の三角形の面積の２倍になるわけだがら、同じ値になる道理である。 この事はまるで蛇足のようだけれども、内外判定に面積を用いる手法もあり、突き詰めればそれとつながっていく。 だが、ここではその関連を示唆するにとどめておく。 なお、面積の２倍になるのはあくまで絶対値で、s値は負の値になることもある。 これについては後で四面体の内外判定のところで詳しく述べる。 　 　重心を用いた同側法 　では、実装がより楽な、重心を用いる方を見てみる。 ssm_2d_tri_g.xlsx　(9.97 KB) 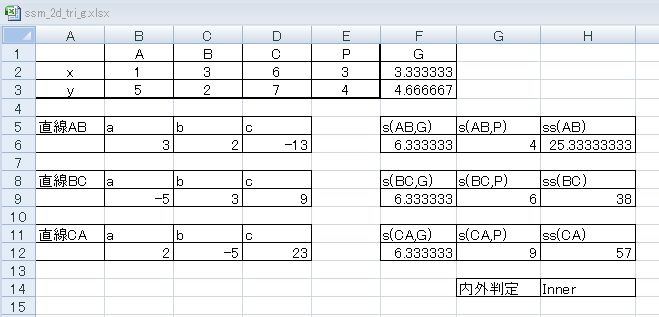こちらは、まずF2、F3セルで重心の座標を計算しておき、F5～F12のエリアでは、各直線と重心Gとの s 値を計算している。 そしてこの値はいずれも 6.333333 となっているが、これは　\( \frac {19} 3 \) であって、三角形ABGの面積が三角形ABCの \( \frac 1 3 \) であることと対応している。\( \frac 1 3 \) になっても符号は同じだから、内外判定には影響がない。 以上、三角形については同側法を使えばごく簡単な計算式の組み合わせで内外判定できることを確認した。 次のページでは、この手法が凸である四角形にも適用可能であることを確認し、さらに任意の凸多角形に応用する場合について考察する。