| はじめに 三角形の頂点の各座標と、ある1点の座標が与えられた時に、その点は三角形の内外いずれにあるか? もちろんこれは人間にとっては紙に描いてみればおおよそわかるけれども、点がほぼ辺の上にあるような時は判断しづらい。一方、コンピュータにとっては「見ればわかる」という事がそもそも無い。 これをコンピュータに判定させるアルゴリズムとしては、外積を用いた方法がよく知られている。しかし外積は高校数学の内容を越え、理解しづらい概念である。 そこで筆者は外積を用いず数学Ⅱの範囲の知識で理解可能なアルゴリズムを考案し、「同側法(the Same Side Method : SSM)」と名付けた。以下その解説と、応用について述べる。 基本的な考え方 例として、3点 A(1,5)、B(3,2)、C(6,7) から成る三角形の内部に、点 P(3,4) がある状況を考える。 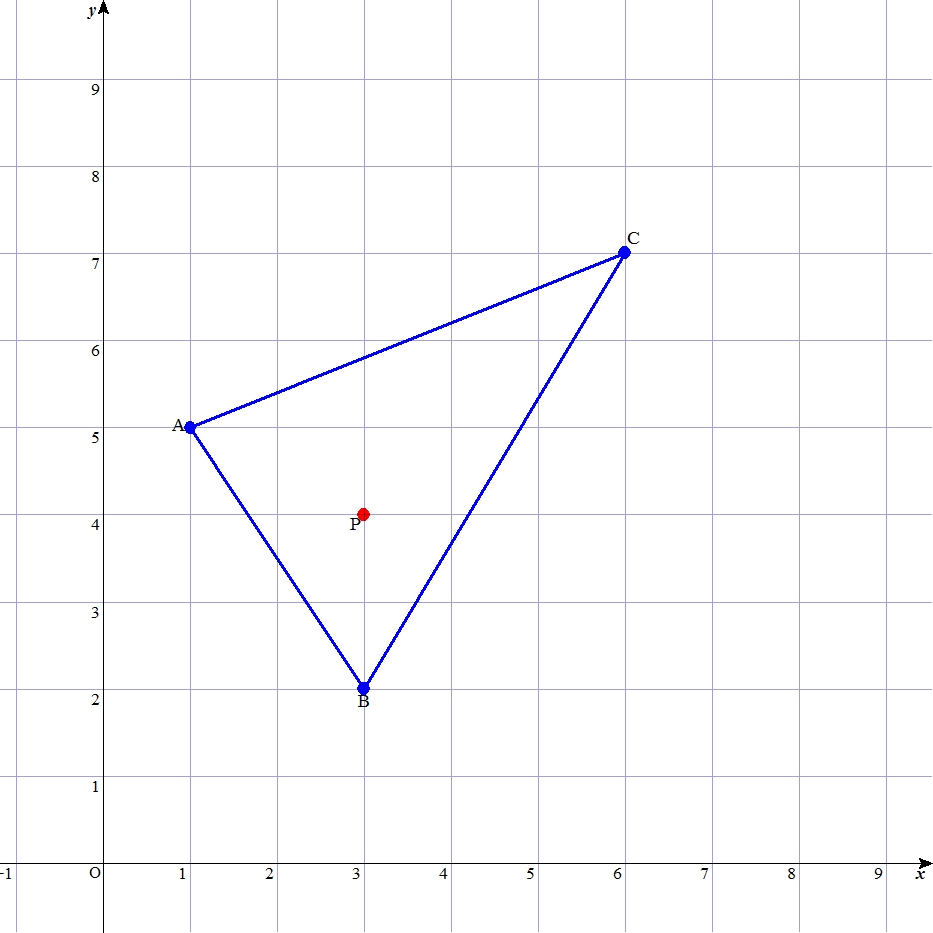 この時、直線ABに注目すると、点Pと点Cは直線ABについて同じ側にある。 逆に、もし異なる側にあれば、点Pは三角形の内部に存在し得ない。 ただし、点Pと点Cが同じ側にあるからと言って、点Pが三角形の内部にあるとは限らない。 この事が保証するのは、点Pが次の図の斜線で示す領域内に存在する、という事である。 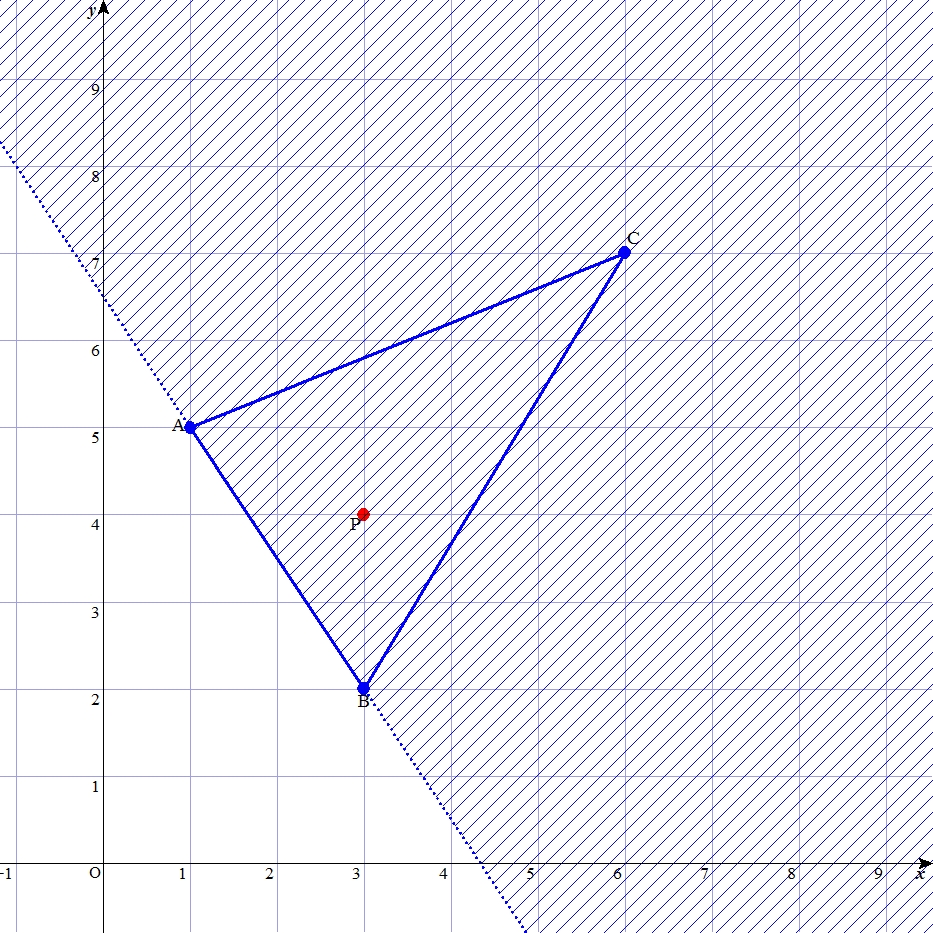 直線BCについても同様に考えると、点Pと点Aが同じ側に存在することは、点Pが下図の斜線領域に存在することを保証する。 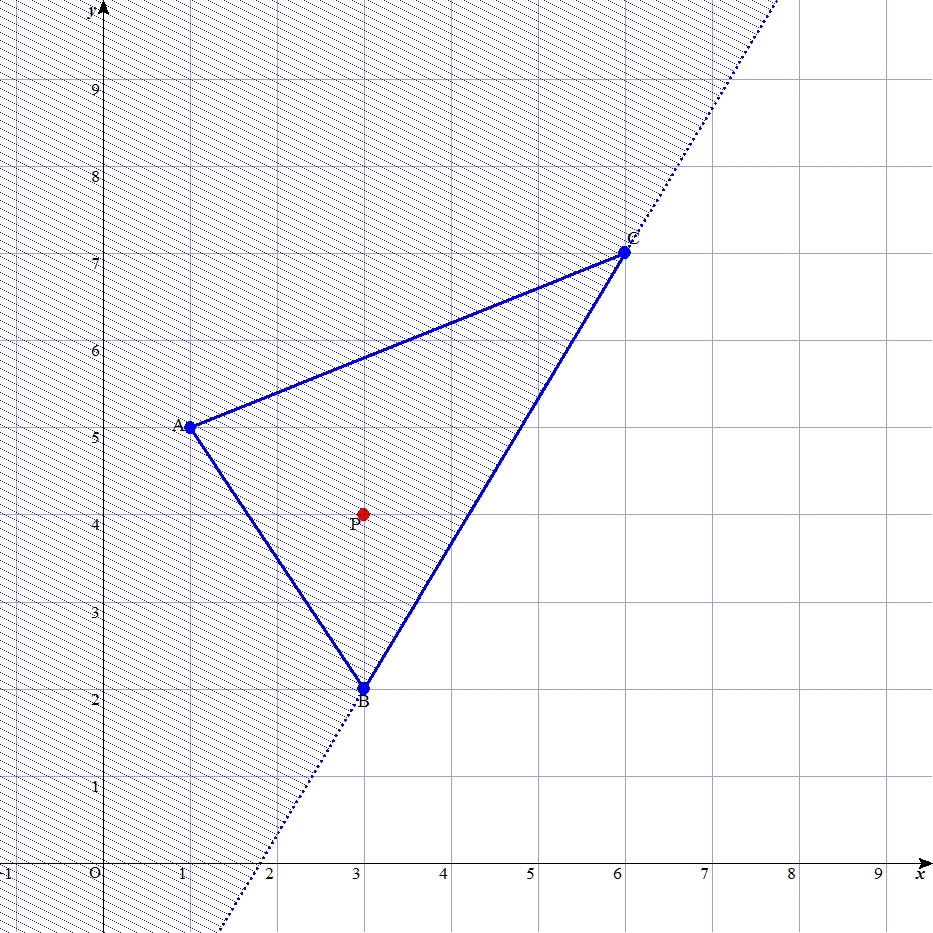 直線CAについても同様である。 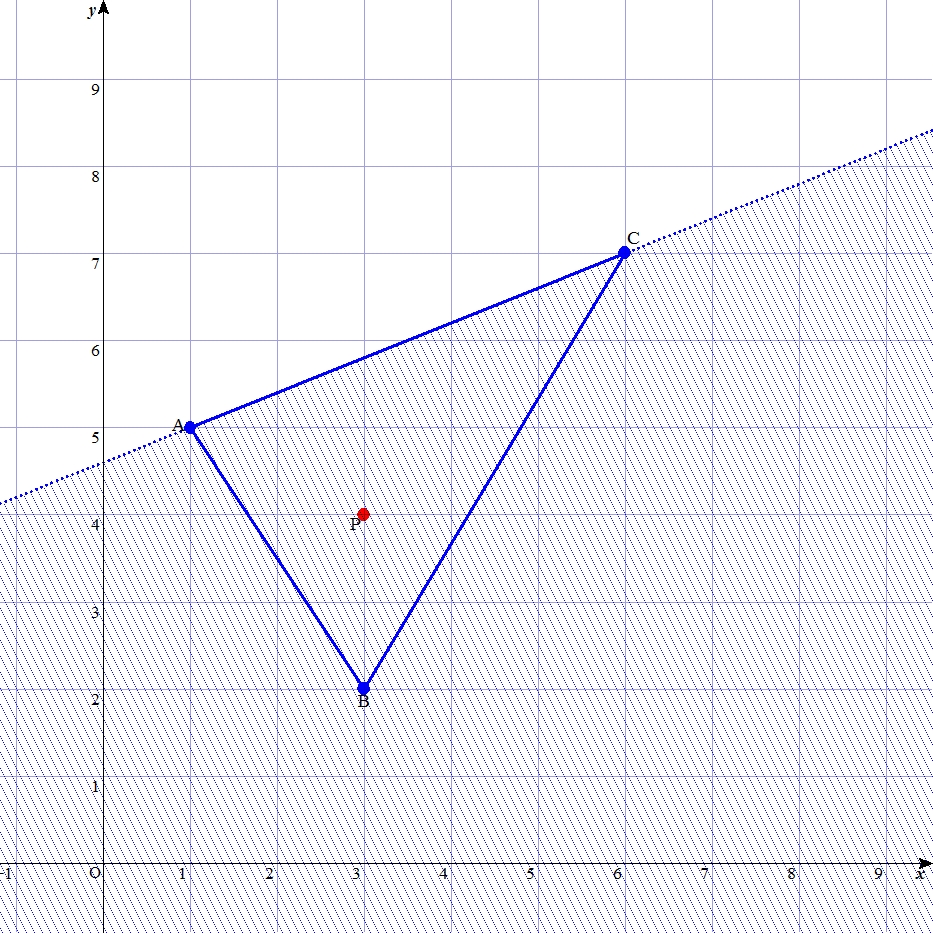 さて、上記の3つの条件がいずれも成り立っている時、点Pは、下図のように三方向の斜線の重なった範囲にしか存在し得ない。そしてそれは他ならず三角形ABCの内部である。 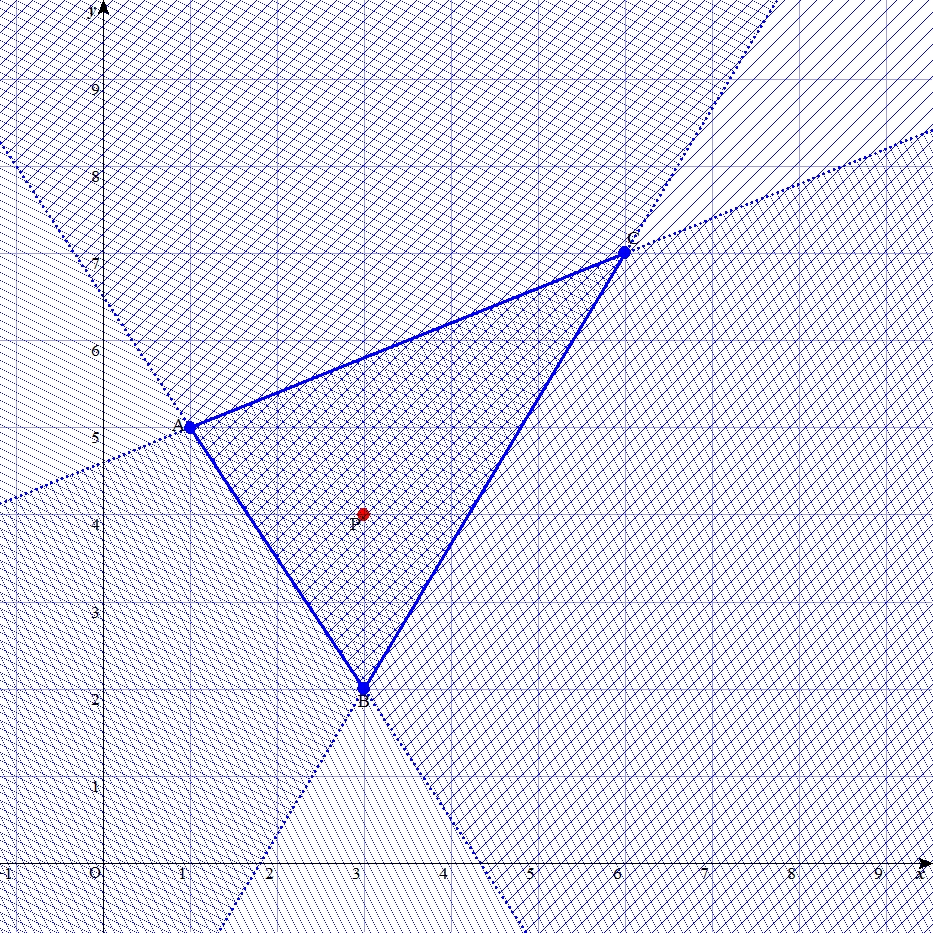 以上のように、直線について2点が同じ側にあるかに注目するのが「同側法」の特色である。 それさえ判定できれば、内外の判定もできる。 「同じ側」の判定 さて、それではどのようにして、同じ側かどうかを判定するか。 それには、高校数学Ⅱで扱われる「点と直線の距離」の公式を応用する。 「点と直線の距離」は、\( ax + by + c = 0 \) の形式で表現された直線と、点\((x_1,y_1)\) 間の距離 \(d\) が、 \( \large d = \frac {| ax_1 + by_1 + c |}{ \sqrt{ a^2 + b^2 }} \) で求められるという公式である。 この公式の証明はベクトル方程式を使った方がわかりやすいのだが、公式の成り立ちを考えると、分子の絶対値記号をとった \(ax_1 + by_1 + c\) の部分は、同じ側に存在する点ならば必ず同符号になる。 ちなみに、点が直線上にあれば、この値はゼロになる。 したがって、2つの点についてこの式の値をそれぞれ算出し、掛け合わせた結果が、 正ならば2点は同じ側 ゼロならば少なくとも1点が直線上 負ならば2点は異なる側 に存在するとわかる。 この値をSS値と呼ぶことにすると、辺BCについての点Aと点P、辺CAについての点Bと点P、辺ABについての点Cと点P、以上3組から3つのSS値を求めることができる。 そして、これらの値から、以下の判断を行う。 まず、一つでも負の値があったら、点は三角形の外部にある。一つも負がなければ、少なくとも外部にはない。 次に、1つでもゼロがあったら、点は三角形の辺または頂点上にある。1つゼロなら辺上、2つゼロなら頂点である。 上記のいずれでもない場合、点は三角形の内部にある。 このように、各辺について、対角の頂点と問題の点が同じ側にあるかを表すSS値を求め、その符号を調べることで内外判定ができる、というのが同側法の要旨である。 ただ、ここまでの説明で対角の頂点を用いてきたのは図を単純にするためで、実は三角形の内部の点であればどこでも良い。SS値を求める際、比較対象が毎回変わるより、同じ点で済めば実装が楽であるから、実際には確実に内部にあるとわかっている1点との比較をした方が良い。三角形において、確実に内部にあり、かつ座標の算出が楽なものとして例えば重心を挙げることができる。 次のページでは上記のアルゴリズムを Excel 上で実装したものを見ながら、関連する事項について考察する。 次ページ 「三角形を対象とした同側法の考察」 |